第二章 宇宙船に働くG(一般相対論と宇宙船)
第1節 荷重とは
この節の内容は他の内容と同様に私が独自の思索を重ねてたどり着いたものである。相対論の本は参考にしたが、一般相対論と宇宙船の加速度について同じ論旨を目にしたことはない。
全く新しいエンジンにより、宇宙船に大きな推力を与えることが可能としても、それにより宇宙船内の人間に大きなGがかかり、それが加速の限界となるのではないかが問題となる。私は、重力もその本質が加速度運動であり、宇宙船の加速度運動と本質を同じくすることを承認する。しかし、宇宙船から人間に伝わる力が徐々に増大し、人間が宇宙船と同じ加速度で運動する場合には、人間は自由に動くことができると考え、以下で説明する。
ロケットが打ち上げられるときには、宇宙飛行士は大きなG(荷重)を経験する。この現象はロケットが上向きに加速度運動することで下向きの重力の壁とぶつかって生じるものと考えられる。私は、荷重は力と力がぶつかって生じると考える。
日常的な経験から言っても、腕を伸ばしたままでいると重く感じるのは下向きの重力に反する力を人体が上向きに与えているからである。足が重く感じるのは地面からの抗力と重力が足でぶつかっているからである。
列車内で列車から人間に伝わる力が徐々に増大する場合にも人体に働くGは次のように説明できる。地球上の物体に働く重力は地球の各部からの万有引力の合力であり、列車の進行方向と反対方向の成分が存在し、その反対方向の成分と列車から伝わる力の間のぶつかり合いが考えられる。また、列車の進行方向も地球の中心方向に完全に垂直ではなく、その影響も考えられる。
そして、人間が空中を自由落下するときに重力加速度が働いているにもかかわらず、人間が自由に運動できるのもこのためである。重力とぶつかる力が無いからである。
ではGはどのように定義されるのか。gを重力加速度とする。1gの地球上でxgで上向きに加速度運動するときに、xGの荷重があるとされる。従って、一般にygの力に抗してxgで加速度運動するときにxyGの荷重があると定義しよう。
第2節 宇宙空間での荷重
これを前提にして宇宙空間で宇宙船から人間に伝わる力が徐々に増大し、人間が宇宙船と同じ加速度で運動する場合の人間にかかるGを考えてみる。
この場合、宇宙船は人間を押した反作用を受ける。従って、推進力と反作用がぶつかりGが生じる。しかし、宇宙空間を飛行しているので人間には宇宙船から伝わった力が作用するだけで力のぶつかり合いは無い。従って、Gは生じないので、人間は自由に動けることになる。この場合、自由落下と同じ状態にあることになる。
但し、宇宙船から人間に伝わる力が急激に増加する場合には、力の変化により人体に大きな荷重が作用することが考えられる。
これに対し、宇宙船からの力が人体を伝わる過程でGが生じるのではないかとの疑問も考えられる。この問題について考えてみる。
人体の質量をmとし、人体のうち一体となっている部分である「mのn分の一の質量の部分」aと一体化していない「残りの部分」bに二分割する。そして、人体は一体化している部分が大きいので、n分の一の部分に最初に宇宙船から力が伝わるものとする。人体の運動する加速度をα、抗力をf、宇宙船から伝わる力をFとする。図2に示した。
図2
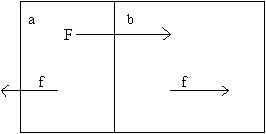
<bについて>
この場合、「残りの部分」bには力のぶつかり合いが無いので、Gが生じないのは前述のとおりである。
<aについて>
問題はn分の一の部分aのGである。
aにxyGが働くものとしてxとyを求めてみる。aはfの力に抗してF─fの力で加速度運動している。
aについて、fがygを与えるので、【8】となる。bについて運動方程式を立てると、【9】となる。【8】と【9】は同じfについての式なので、【10】となる。これを整理してyは、【11】となる。
人体が加速度αで運動しているので、【12】となる。従って、xは【13】となる。
【11】と【13】からxyを求めると、【14】となる。
【14】より、nが1に近づくほど、すなわち、人体の一体である部分が大きいほど、Gは小さいことになる。そして、人体は非常に緊密に一体化していると言えるので、nマイナス1はほとんど0に近くなる。従って、荷重もごく小さくなる。人体各部に働く荷重は0か、0にごく近いこととなる。
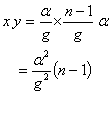 【14】 【14】 |
第3節 重力下での荷重
以上と比較するために、地球上のロケット打ち上げのときの人体にかかるGについて同じように考察してみる。
この場合も人体の質量をmとし、一体化している「mのn分の一の質量の部分」cと一体化していない「残りの部分」dに二分割し、n分の一の部分に最初に、ロケットから力が伝わるものとする。図3に示した。
図3
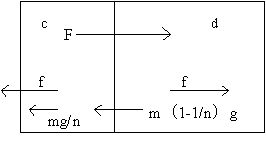
<dについて>
この場合、「残りの部分」にも当然重力が働き、力のぶつかり合が生じるので、Gが生じる。
dにxyGが働くものとして、xとyを求めてみる。
dが1gの重力に抗して、加速度αで運動していることになるので、【16】【18】となる。従って、yは【17】、xは【19】となる。ゆえにxyは【20】となる。
<cについて>
cにxyGが働くものとして、xとyを求めてみる。
xはcがdと同じく加速度αで運動しているので、【19】となる。
yについて考えると、【21】となる。cについて運動方程式を考えると、【22】となる。また、人体全体について運動方程式を立てると、【23】となる。【21】を【22】に入れると、【24】となる。【24】から【23】を使ってFを消去すると、【25】となる。【25】を整理して、yを求めると、【26】となる。
【19】と【26】からxyを求めると、【27】となる。
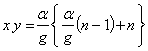 【27】 【27】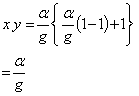 【28】 【28】 |
【27】において、nが1に近づくほど、Gは小さくなるが、α/gよりは小さくならないことになる。仮に、nが1に等しいとすると、【27】は【28】となる。従って、人体各部に働く荷重は【20】と【28】より、α/gより大きい値となる。
以上から明らかなように、重力下では一定の値以上の荷重が働くのに対して、宇宙空間では荷重がごく小さいことになる。
さらに、人体と宇宙船との間の万有引力も存在するが、微小として無視した。