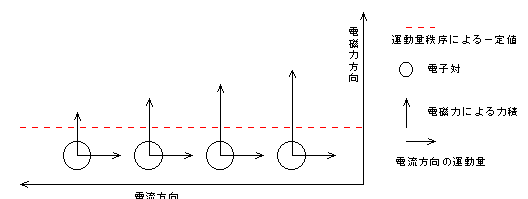
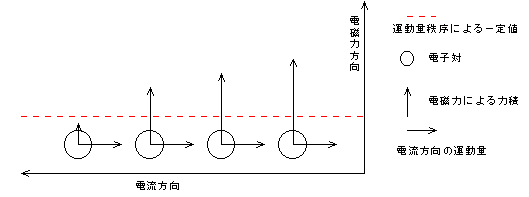
第3章 運動量秩序の拡張

 

 

いままで、運動量秩序が扱う電子対の運動量は永久電流が流れる方向（以後、「電流方向」と略します）のみを念頭においてきました。それを永久電流に外部磁場が働いて電磁力が生じる方向（以後、「電磁力方向」と略します）の運動量にまで、私の独創により拡張しました。

 

この拡張を行わないとどのようなことが生じるか、考えます。

 

基本:力積と運動量

力積とは「力×時間」です。力をF、時間をTとすると、力積はFTで表されます。

力とは「質量×加速度」です。

質量をM、加速度をαとすると、F=Mαとなります（ニュートンの運動の法則）。

運動量は「質量×速度」ですので、速度をVとすると、運動量はMVで表されます。

力積と運動量は等しい関係にあります。

F＝Mαの両辺にTをかけます。

T×F=Mα×T

左辺は力積を示しています。

右辺について考えます。

速度は「加速度×時間」ですので、V＝α×Tとなります。

これを右辺に代入します。

FT＝MVの関係が成立します。

したがって、永久電流に加えられた力積が電子対の運動量になります。

永久電流に外部磁場が働いて生じる電磁力による力積も運動量に変化することになります。

 

外部磁場の強さは一様ではないことがあります。外部磁場の強さが一様ではないため、永久電流を構成するそれぞれの電子対に一定時間内に異なる大きさの力積が与えられたとします。

 

図6 異なる大きさの力積が電子対に加えられた場合a

 

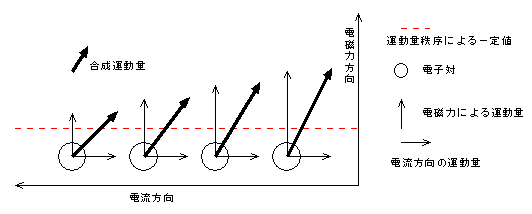
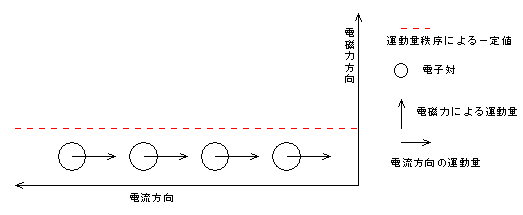
この力積がそのまま運動量に変化したとします。

 

図7 異なる大きさの力積が運動量に変化した結果a

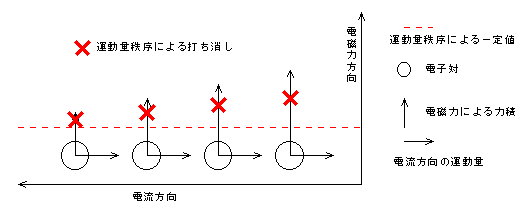
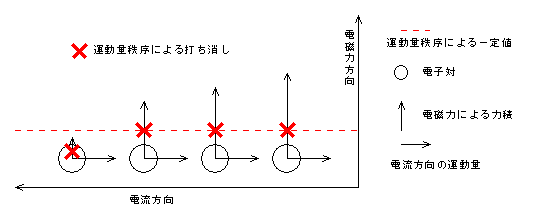
電流方向の運動量と電磁力方向の運動量を合成した電子対が全体として持つ運動量の大きさがバラバラになってしまいます。これでは、各電子対が同じ運動量を持ち、各電子対が一斉に同じ運動量に変化することができません。電気抵抗が生じて永久電流が崩壊してしまいます。

そこで、電磁力方向にも運動量秩序の規制が働きます。これにより、電子対の重心運動の運動量に変化できない力積が生じます。そして、変化できないこととなった力積は、他のエネルギーに転化すると考えます。他のエネルギーとは、電子対の重心運動ではない、各電子の運動や振動のエネルギーです。しかし、このエネルギーによる熱を心配する必要はありません。このエネルギーが加わっても、クーパー対のミクロな運動に不規則・乱雑性が無いことには変わりありません。クーパー対の集合である永久電流は電気抵抗ゼロで永久的に流れ続けます。抵抗ゼロであるということは、抵抗により生じる熱もゼロであるということです。クーパー対は熱には寄与しないのです。そして、これらのエネルギーは、振動自体に必要なエネルギーとして消費されたり、反平行運動を維持するためのエネルギーとして消費されたりします。その残りのエネルギーが、操作して超伝導磁石を常伝導状態に切り替えた後に、最終的に熱として放出されることがあるということです。

 

図8  異なる大きさの力積に働く運動量秩序の規制a

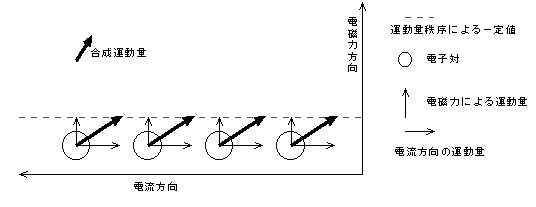
「運動量秩序による一定値」以上の力積が重心運動の運動量に変化できません。

 

図9  異なる大きさの力積に運動量秩序の規制が働いた結果a

この結果、電子対が全体として持つ運動量が同じ大きさに一斉に変化し、運度量秩序が成立し、永久電流は永久的に流れ続けます。

それから、電磁力が働いて電子対に与えられる力積の最小のものが、一定時間内に一定の値に満たない場合は、すべての力積が運動量に変化できないと考えます。一定の値を考えるのは電子対も量子だからです。超伝導はマクロな量子現象なのです。そして、一定の時間を考えるのは、その時間内に重心運動の運動量に変化しなければ、重心運動を変化させる力積として用をなさなくなると考えるからです。ですから、その一定の時間内に与えられた力積が次の一定の時間内も重心運動に変化しなければ、すべて他のエネルギーに転化することになります。

 

図10 異なる大きさの力積が電子対に加えられた場合b

これでは図7のように合成した運動量がバラバラになります。

 

図11 異なる大きさの力積に働く運動量秩序の規制b

全力積に運動量秩序による規制が働きます。

 

図12 異なる大きさの力積に規制が働いた結果b

全力積が運動量に変化できません。